04. Linear Regression - Least Square
Least Square
먼저 이번 글을 통해 Least Square 방식에 대해서 알아보자!
우선 우리가 Least Square를 수행하는 목적은 아래 가설함수(Hypothesis)의 Cost function을 최소화 하는 것이다.(이전 글 참고)


Cost 함수 J의 실제 그래프가 아래와 같다 가정을 해보자.

우리는 Least Square을 사용해서 아래 사진과 같이 Cost Function이 가장 낮게 나오는 (𝜃1,𝜃2) 값을 찾아볼 것이다.

최소제곱법에서는 이 Cost 함수를 최소화하는 𝜃1와 𝜃2를 찾기 위해 미분을 사용한다.
아래와 같이 미분을 통해 Cost 함수의 기울기가 0이 되는 지점, 즉 최소값을 갖는 지점을 찾을 수 있다.

그리고 이 값들이 바로 최적의 𝜃1와 𝜃2, 즉 우리가 찾고자 하는 선형 회귀 모델의 파라미터가 된다.
다음으로, 최소제곱법이 선형회귀문제를 해결하기 위한 일반적인 방법인 이유를 알아보자.
최소제곱법은 선형대수학의 '정규방정식(Normal Equation)'을 통해 연산을 단순화 할 수 있다는 큰 장점이 있다.
정규방정식은 선형 회귀 문제에 대한 해를 직접적으로 계산하는 방법을 제공한다.
미분을 통해 오차 제곱의 합을 최소화하는 방법과는 대조적으로, 정규방정식은 다음의 수식을 통해 최적값을 직접 계산한다.

여기서 X는 입력 변수 행렬, y는 출력 변수 벡터, T는 전치(transpose), -1은 역행렬(inverse)을 의미합니다.
이 식을 통해, 우리는 직접적으로 최적의 𝜃를 구할 수 있습니다.
이 방식은 미분을 통해 오차 제곱의 합을 최소화하는 방식과 동일한 결과를 주지만, 복잡한 계산이나 반복 과정 없이 바로 결과를 얻을 수 있다는 장점이 있습니다.
그런데 여기서 주의할 점은, 이 방법이 항상 적용 가능한 것은 아니라는 점이다.
특히 선형이 아닌 비선형 모델에서는 이 방법이 그대로 작동하지 않는다.
(최소제곱법의 선형성은 회귀 계수(여기서는 𝜃1, 𝜃2)에 대한 선형성을 의미하며, 독립 변수에 대한 선형성을 의미하지는 않습니다.)
선형모델과 비선형모델의 구분
선형 모델 vs 비선형 모델
선형 모델과 비선형 모델의 구분이 헷갈려 추가로 작성해놓았다.
우선, 아래 그림에서 왼쪽이 선형모델일까? 오른쪽이 선형모델일까?
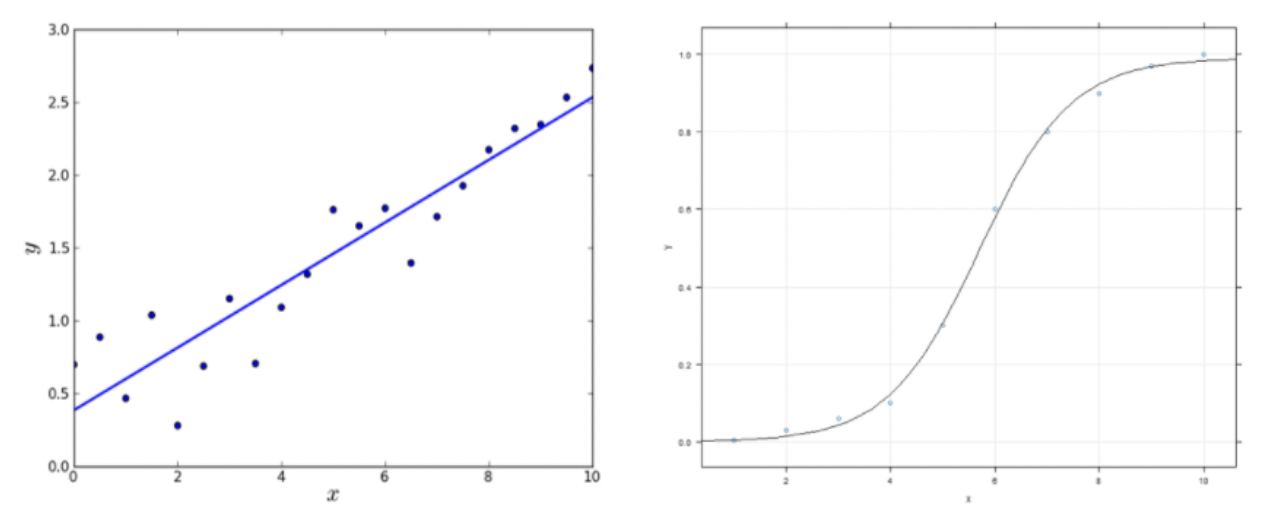
정답: 둘다 선형모델로 표현이 가능하고, 선형모델이 될 수 있다.
선형모델의 정의부터 알아보자.
1. 선형모델이란?
- 선형모델이란 "머신러닝 공식에서 계수들이 선형결합의 관계에 있을 때의 모델"을 말한다.
- 선형결합이란 "두개의 벡터의 합"을 의미한다.
- 또한, 선형모델은 언제나 직선모양으로 그려지지 않는다. 위에서 언급한대로 가중치들이 선형결합을 하고 있으며, 선형모델이 되기 때문에 곡선인 그래프가 그려질수도 있다.
즉, '가중치가 어떻게 결합되어 있는지에 따라서 선형이 되고 안되고 결정된다'라고 정의 할 수 있습니다.
2. 비선형모델이란?
- 비선형 모델이란 "데이터를 어떻게 변형하더라도 파라미터를 선형 결합식으로 표현할 수 없는 모델"을 말합니다.
비선형 모델에 대한 예를 들어보자.
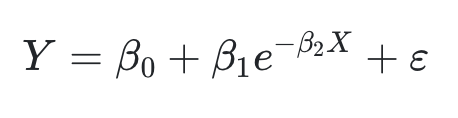
위 식의 경우 β0에 대해 편미분을 하였을 때, '∂f/∂β0 = 1'로 상수이므로 모형식이 β0에 대해서는 선형이다.
하지만 β1 ,β2에 대한 미분 결과는 미분대상(ex. β1에 대한 미분)이 아닌 계수들을 변수로 여전히 포함하고 있으므로 β1, β2에 대해서는 전체적으로 비선형모델이 됩니다.

3. 간단한 O, X퀴즈로 개념을 정리해보자
- 선형은 변수 x의 1차 다항식을 의미하는 것이 아니다.
- 선형모델은 모두 직선으로만 그려진다.
- 곡선으로 그려진 그래프는 선형모델이 될 수 없다.
- 선형과 비선형을 나누는 기준은 계수들의 결합에 따라서 달라진다.
정답 : O, X, X, O
그 이유는, 비선형 모델에서는 Cost Function이 볼록 함수의 형태를 띠지 않을 수 있고, 따라서 여러 개의 Local Minimum을 가질 수 있기 때문이다.

이런 경우, 최소제곱법을 통해 찾은 해는 local minimum일 뿐, 전역 최소값(global minimum)을 보장하지 않는다.
그렇다면 복잡한 비선형 문제를 어떻게 해결할 수 있을까?
바로 이 문제를 해결하기 위한 도구가 다음 글에서 다룰 Gradient Descent(경사하강법)이다.
다음 글에서 계속...